הוכחת משפט בגיאומטריה: אם שני ישרים מקבילים נחתכים על-ידי ישר שלישי, אזי סכום שתי זוויות חד-צדדיות פנימיות הוא 180º
הוכחת משפט בגיאומטריה: אם שני ישרים מקבילים נחתכים על-ידי ישר שלישי, אזי סכום שתי זוויות חד-צדדיות פנימיות הוא 180º
נתונים שני ישרים מקבילים a, b וחותך היוצר זויות 1,2 בין הישרים לחותך.
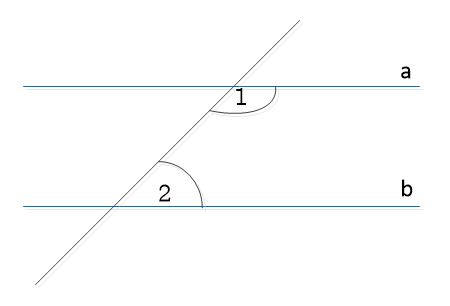 |
| זויות חד צדדיות פנימיות, סכומן 180 מעלות |
הוכחה
משפט זה ניתן להגדיר על דרך השלילה של אקסיומת הישרים המקבילים. אם שני ישרים הנחתכים על-ידי ישר שלישי אינם יוצרים באף צד של החיתוך זוג זוויות פנימיות שסכומן קטן מ- 180º, אזי שני הישרים לעולם לא יפגשו גם אם נאריכם עד לאינסוף. כלומר, במקרה שלעיל שני הישרים הם ישרים מקבילים.





