סדרה חשבונית – נוסחה לאיבר הכללי

Spread the love

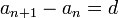
סדרה חשבונית היא סדרה של מספרים, שבה ההפרש בין כל שני איברים עוקבים הוא קבוע: $\ a_{n+1}-a_n=d$
דוגמה: בסדרה 3, 5, 7, 9, 11, … (מימין לשמאל) ההפרש הקבוע בין כל שני איברים עוקבים הוא 2.
סדרה חשבונית מוגדרת באמצעות שלושה מאפיינים:

האיבר הראשון בסדרה.
ההפרש הקבוע בין שני איברים עוקבים בסדרה.
מספר האיברים בסדרה (שעשוי להיות סופי או אינסופי).

לפי מאפיינים אלה ניתן לדעת מהו כל אחד מאיברי הסדרה.

נוסחה לאיבר הכללי
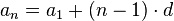אם $a_1$ הוא האיבר הראשון, ו־ $d$ הוא ההפרש, האיבר ה־ $n$ נתון על ידי הנוסחה: $a_n=a_1+(n-1) \cdot d$ .

דוגמאות:

דוגמא 1 – מציאת האיבר הכללי

נתונה הסדרה החשבונית: … 8, 5, 2
מצא את האיבר ה- 11 בסדרה:
נמצא תחילה את הפרש הסדרה d, נשתמש למשל בהרש האיברים השני והראשון :

ע"פ נוסחת האיבר הכללי בסדרה חשבונית: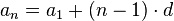
$a_n=a_1+(n-1) \cdot d$
עבור האיבר ה- 11 , n = 11 ולכן:

דוגמא 2 – מציאת האיבר הראשון בסדרה:
נתונה סדרה חשבונית שבה האיבר ה- 6 הוא:
והפרש הסדרה

מצא את האיבר הראשון בסדרה:
ע"פ נוסחת האיבר הכללי: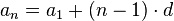
$a_n=a_1+(n-1) \cdot d$
נחלץ את

דוגמא 3 – מציאת הפרש הסדרה d

מצא הפרש סדרה חשבונית (d) שבה האיבר ה- 13 שווה 77 והאיבר הראשון הוא 5
נתון לנו כי

מספר האיברים בסדרה הוא 13 ,
ע"פ נוסחת האיבר הכללי: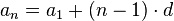
$a_n=a_1+(n-1) \cdot d$
נחלץ את ההפרש d:

נציב ונקבל את הפרש הסדרה d:

קישורים:
הוכחת נוסחאות למציאת סכום סדרה חשבונית ודוגמא פתורה

תרגיל פתור סדרה חשבונית – מציאת הפרש סדרה ואיברה הראשון ע"פ קשרים בין איברים בה – תרגיל – בסדרה חשבונית האיבר השביעי גדול פי 4 מהאיבר השלישי וסכום האיברים השלישי והרביעי גדול ב – 1 מהאיבר החמישי. מצא את הפרש הסדרה החשבונית…