חרוט ישר – שטח בסיס, מעטפת, נפח

Spread the love

חרוט, או חדודית, קרוי גם קוֹנוּס (מיוונית: κώνος) הוא גוף תלת-ממדי, המוגדר על ידי בסיס כלשהו, הקרוי ה"מכוון" של החרוט, ונקודה במרחב, שאינה שייכת לבסיס ("קודקוד החרוט"). החרוט מתקבל כאוסף כל הנקודות הנמצאות על קטעים ישרים הנמתחים בין הבסיס לקודקוד. עצם אשר צורתו כשל חרוט מתואר כ"חרוטי" או כ"קוני".
גובה החרוט הוא הקטע המתחיל בקודקוד החרוט והמאונך למישור העובר דרך בסיסו. גם אורך הקטע מתואר בשם "גובה".
פעמים רבות משתמשים בשם "חרוט" או "חרוט ישר" לציון חרוט שבסיסו עיגול וגובהו עובר במרכז העיגול (הקודקוד נמצא בדיוק "מעל" מרכז המעגל). חרוט ישר מתקבל על ידי סיבוב משולש ישר-זווית סביב ציר (שמתלכד עם הגובה). חרוט עיגולי שצירו אינו מאונך לבסיסו קרוי חרוט משופע.

פני החרוט הם משטח ישרים.
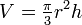הנפח $V$ של חרוט שגובהו $h$ ושטח בסיסו $S$ הוא $V=\tfrac{1}{3}Sh$ . בפרט הנפח של חרוט עיגולי שלבסיסו רדיוס $r$ הוא 1/3 מנפחו של גליל בעל אותם ממדים, כלומר $\ V = \tfrac{\pi}{3} r^2 h$ .

שטח פניו של חרוט עיגולי הוא $\ A = \pi r (r + s)$ , כאשר $s = \sqrt{r^2 + h^2}$ הוא "גובה השיפוע" של החרוט (לפי משפט פיתגורס). הביטוי הראשון בנוסחת השטח, $\pi r^2$ , הוא שטח בסיסו, והביטוי השני $\pi r s$ , הוא שטח פני הצד. פני שטחו = שטח הבסיס + שטח הצד.

דוגמא
נתון חרוט ישר שרדיוס בסיסו 5 = r ס"מ וגובהו 8 = h ס"מ. חשב את שטח בסיסו, גובה השיפוע, שטח פני הצד, שטח פניו ונפחו.

פתרון

שטח בסיס החרוט הוא שטח עיגול שרדיוסו r = 5 ס"מ, לכן:
שטח בסיס החרוט הוא 78.5 סמ"ר

גובה השיפוע s של חרוט ישר הוא אורך הקטע היוצא מקודוקד החרוט אל המעגל המקיף בסיסו וגודלו:
$s = \sqrt{r^2 + h^2}$ כאשר r הוא רדיוס בסיס החרוט ו- h גובה החרוט.

גובה השיפוע של החרוט הוא 9.43 ס"מ.

שטח פני הצד ST של החרוט הוא שטח המעטפת (ללא שטח הבסיס העגול) ושווה ל:
כאשר r רדיוס בסיס החרוט ו- s גובה השיפוע:
שטח פני צד החרוט הוא 148.05 סמ"ר.

שטח פני החרוט הוא סכום שטח הבסיס ושטח פני הצד: פני שטחו = שטח הבסיס + שטח הצד
פני שטחו = 78.5 + 148.05 = 226.55 סמ"ר

נפח החרוט הישר נתון בנוסחה: 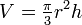$\ V = \tfrac{\pi}{3} r^2 h$ (שטח בסיס החרוט כפול גובהו לחלק לשלוש)

לכן:

נפחהחרוט הוא 209.33 סמ"ק

חרוט ישר – שטח בסיס, מעטפת, נפח

salome

השופט ארז פורת גזר 8 שנות מאסר לנהג ערבי שהשתמש בחשיש וגרם לתאונת דרכים קטלנית בה נהרגו אמא ובנה והנהג נפצע גם הוא ת"פ 47794-06-17 מד"י נ' ג'האד סאלח

אלן רוס מוריסון נעצר עד תום הליכים על התעללות בכלבו אמש מ"ת 10687-10-20

הפרקליטה הילה בנסון בסמן שיקרה את השופט אבי גורמן שהאזרח יגאל מסיכה איחר להגיש השגה על שומת מע"מ וניסתה לסחוט 520,000 ש"ח על חוב מע"מ פיקטיבי ע"מ 19458-04-20

עו"ד קובי דוידוביץ קצין התגמולים של צה"ל התעלל בנכי צה"ל והתרשל בטיפול. דוד רוזן סגר התלונה כדי לא לפגוע לו במינוי לשפיטה

הפסד צורב לפרקליטה שירלי אקרמן הרדיפה האובססיבית שלה אחרי רפי רותם עלתה למדינה 260,000 ש"ח בגין "רשלנות היברידית" ת"א 59471-01-17

גרושה העלילה על אבא שהוא פדופיל מנעה ממנו קשר עם בנו (בן 12) 8 שנים והגישה נגדו תלונות שווא במשטרה תפצה אותו ב-180 אלף ש”ח תלה”מ 51455-03-17

כתיבת תגובה לבטל